2352 반도체 설계

www.acmicpc.net/problem/2352

[

2352번: 반도체 설계

첫째 줄에 정수 n(1 ≤ n ≤ 40,000)이 주어진다. 다음 줄에는 차례로 1번 포트와 연결되어야 하는 포트 번호, 2번 포트와 연결되어야 하는 포트 번호, …, n번 포트와 연결되어야 하는 포트 번호가 주

www.acmicpc.net

](https://www.acmicpc.net/problem/2352)

(문제 풀이)

해당 문제의 요구사항

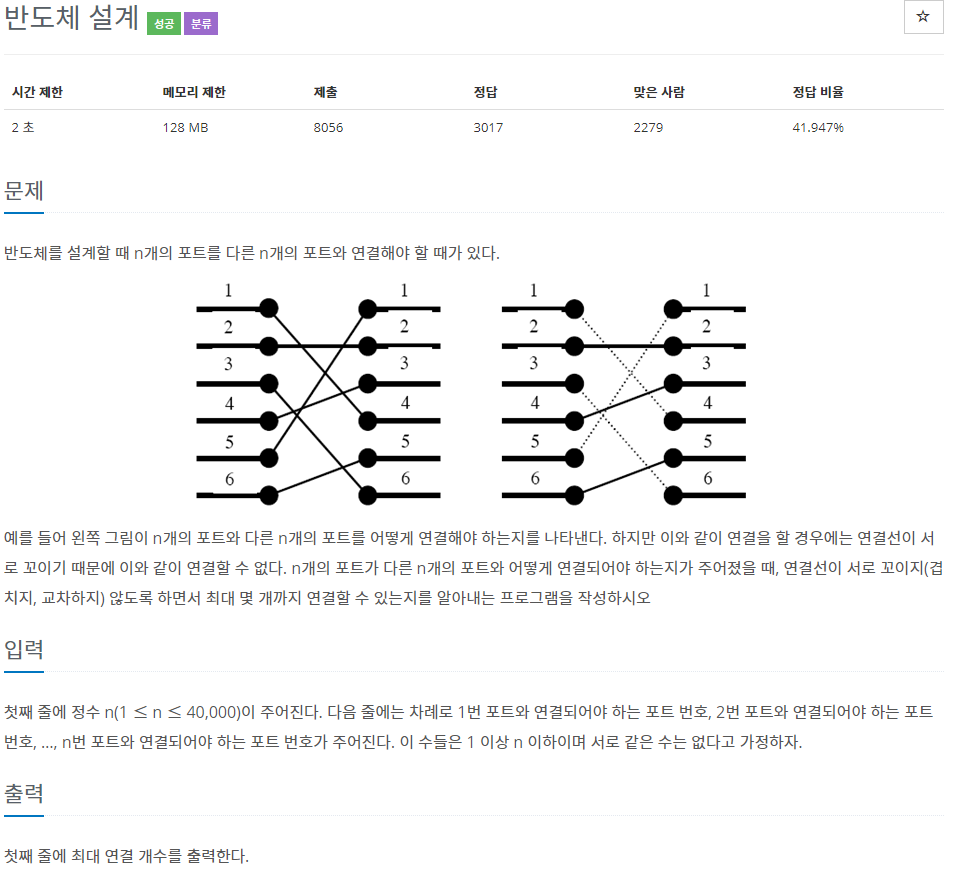
• 왼쪽의 포트들을 오른쪽의 포트로 겹치지 않게 가장 많이 연결할때의 포트 갯수를 구한다.

1. 가장 쉽게 생각 해볼 수 있는 최선의 방법은, 시작 포트에서 부터 가장 적은 번호와 연결시키는 방법일 것이다.
2. 가장 최악의 경우를 생각해보면 가장 첫번째 포트가 가장 마지막 포트와 연결 되는 경우이다.
   (위 그림에서 6으로 시작한다면 그 이후에 나오는 왼쪽 포트에서 선을 뽑을 수가 없게 된다.)

• 위 그림에서 최상의 경우 ( 왼쪽의 포트에서 오름차순으로 숫자를 나열 한 경우) 
   { 2,3,5} (3개)
  
  이 문제의 조건으로 추론해볼 수 있는 방법은 가장 긴 증가하는 부분 수열을 나타내는 것이다.
  
  
• 또한 문제에서 최대 포트가 4만개(40,000)개이므로 단순히 O(N^2)으로 접근하면 당연히 시간초과가 난다.

따라서, n logn 으로 사용할 수 있는 LIS를 구현해야한다. c++에서 제공되는 lower_bound를 이용하면 쉽게 구할 수 있다. lower_bound의 내부는 이분탐색을 하여 찾고자 하는 값의 가장 첫번째 인덱스 또는 그게 없다면 그거보다 한 단계 큰 수의 첫 번째 인덱스를 반환하게 된다. (하한값 찾기)

따라서 포트의 갯수 마다 이분탐색을 실시하는것으로 n log n 에 찾을 수 있다.
실제 어떤 값이 들어가 있는지보다 몇개가 들어가있는지 길이가 곧 문제서 요구하는 해가 된다.

#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
using namespace std;
vector<pair<int,int>> v;
int N;
int main(void)
{
	cin >> N;
	for (int i = 0; i < N; ++i)
	{
		int a = 0;
		cin >> a;
		v.push_back({a,i + 1 });

	}
	sort(v.begin(), v.end());
	vector<int> list;
	for (int i = 0; i < N; ++i)
		list.push_back(v[i].second);
	
	vector<int> ans;
	ans.push_back(list[0]);
	for (int i = 1; i < N; ++i)
	{
		if (ans.back() < list[i])
			ans.push_back(list[i]);
		else
		{
			auto it = lower_bound(ans.begin(), ans.end(), list[i]);
			*it = list[i];
		}
	}

	cout << ans.size() << '\n';
	return 0;
}