728x90
https://www.acmicpc.net/problem/15685
15685번: 드래곤 커브
첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커�
www.acmicpc.net

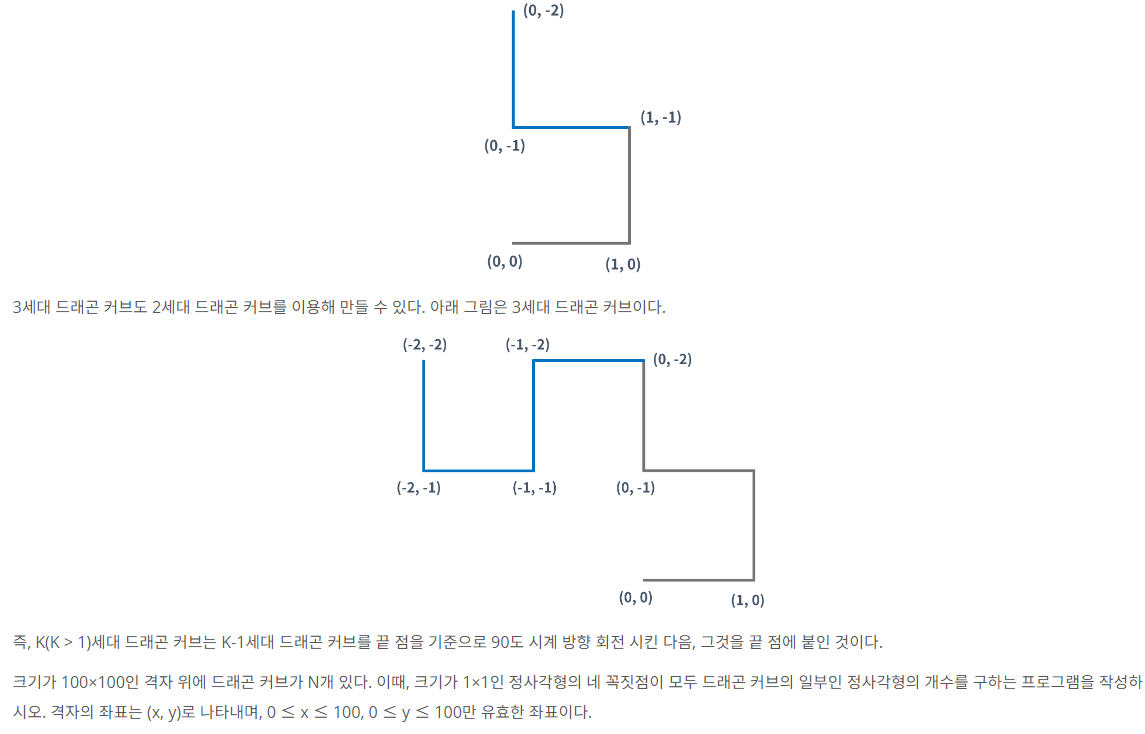

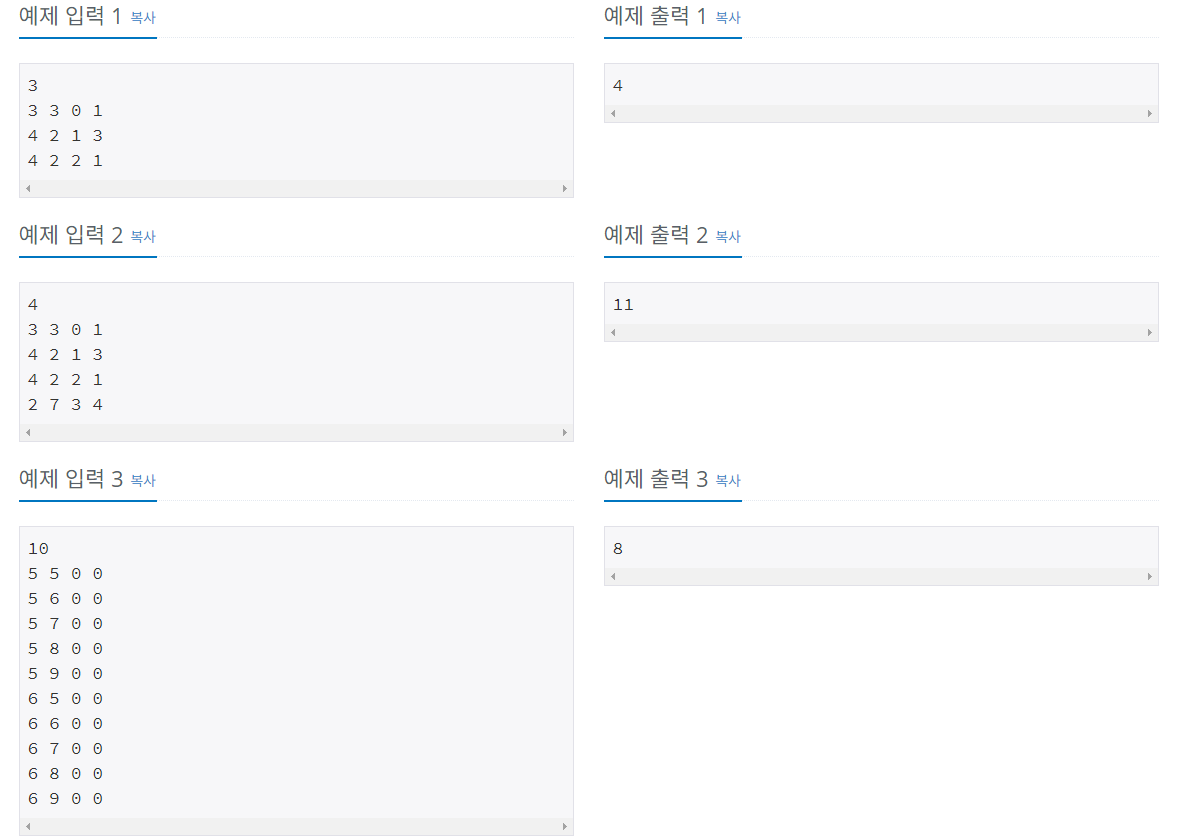

(풀이)
규칙을 찾는것이 가장 중요하다.
만약 0세대가 0부터라면
1세대는 0,1
2세대는 0,1,2,1
3세대는 0,1,2,1,2,3,2,1
이전 세대의 끝에서부터 처음 인덱스까지 반대숫자를 하나 더해주며 나열해주면 된다.
(역순 +1 )
3이 넘어가면 1이 되므로 모듈 연산자를 통해 보정을 해주었다.
#include<iostream>
#include<vector>
#include<stack>
using namespace std;
void Input();
void Solve();
vector<int> Get_DrangonDir(int dir, int generation);
void move_Dragon(int x, int y, vector<int> &v);
void OutputResult();
int N;
int map[101][101];
int dx[] = { 1,0,-1,0 };
int dy[] = { 0,-1,0,1 };
int ans;
struct D
{
int x;
int y;
int start_dir;
int generation;
};
vector<D> dragon_info;
int main(void)
{
Input();
Solve();
return 0;
}
vector<int> Get_DrangonDir(int dir, int generation)
{
vector<int> dir_sequence;
dir_sequence.push_back(dir);
for (int j = 0; j < generation; ++j)
{
stack<int> s;
for (int k = 0; k < dir_sequence.size(); ++k)
{
s.push(dir_sequence[k]);
}
while (!s.empty())
{
int next_dir = s.top();
s.pop();
next_dir = (next_dir + 1) % 4;
dir_sequence.push_back(next_dir);
}
}
return dir_sequence;
}
void move_Dragon(int x, int y, vector<int> &v)
{
map[y][x] = true;
int xn = x;
int yn = y;
for (int i = 0; i < v.size(); ++i)
{
int dir = v[i];
xn += dx[dir];
yn += dy[dir];
map[yn][xn] = true;
}
}
void Solve()
{
for (int i = 0; i < dragon_info.size(); ++i)
{
int x = dragon_info[i].x;
int y = dragon_info[i].y;
int dir = dragon_info[i].start_dir;
int g = dragon_info[i].generation;
//¼¼´ë ¸¸Å ¹Ýº¹
vector<int> dir_list = Get_DrangonDir(dir, g);
move_Dragon(x, y, dir_list);
}
OutputResult();
}
void OutputResult()
{
for (int i = 0; i <= 100; ++i)
{
for (int j = 0; j <= 100; ++j)
{
if (map[i][j] && map[i][j + 1] && map[i + 1][j] && map[i + 1][j + 1])
ans += 1;
}
}
cout << ans << '\n';
}
void Input()
{
cin >> N;
int x, y, dir, g;
D node;
for (int i = 0; i < N; ++i)
{
cin >> x >> y >> dir >> g;
node.x = x;
node.y = y;
node.start_dir = dir;
node.generation = g;
dragon_info.push_back(node);
}
}
300x250
'Algorithm > 시뮬레이션(구현)' 카테고리의 다른 글
| 17144 미세먼지 안녕! (0) | 2020.12.07 |
|---|---|
| 14891 톱니바퀴 (0) | 2020.08.07 |
| 17140 이차원 배열과 연산 (0) | 2020.08.07 |



댓글