728x90
https://www.acmicpc.net/problem/1912
1912번: 연속합
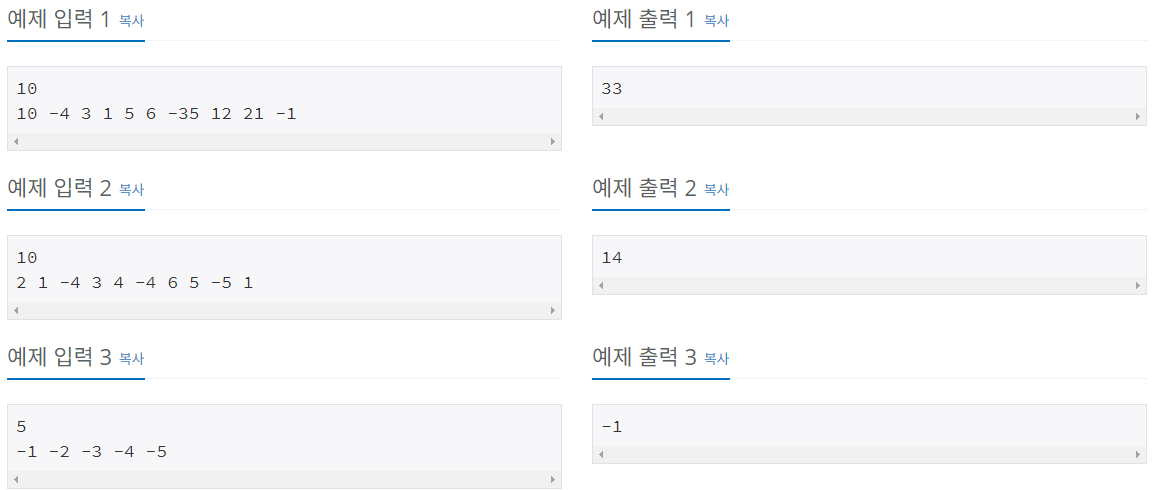
첫째 줄에 정수 n(1 ≤ n ≤ 100,000)이 주어지고 둘째 줄에는 n개의 정수로 이루어진 수열이 주어진다. 수는 -1,000보다 크거나 같고, 1,000보다 작거나 같은 정수이다.
www.acmicpc.net
연속합 성공
시간 제한메모리 제한제출정답맞은 사람정답 비율
| 2 초 | 128 MB | 63872 | 18053 | 12373 | 27.407% |
문제
n개의 정수로 이루어진 임의의 수열이 주어진다. 우리는 이 중 연속된 몇 개의 수를 선택해서 구할 수 있는 합 중 가장 큰 합을 구하려고 한다. 단, 수는 한 개 이상 선택해야 한다.
예를 들어서 10, -4, 3, 1, 5, 6, -35, 12, 21, -1 이라는 수열이 주어졌다고 하자. 여기서 정답은 12+21인 33이 정답이 된다.
입력
첫째 줄에 정수 n(1 ≤ n ≤ 100,000)이 주어지고 둘째 줄에는 n개의 정수로 이루어진 수열이 주어진다. 수는 -1,000보다 크거나 같고, 1,000보다 작거나 같은 정수이다.
출력
첫째 줄에 답을 출력한다.
<풀이>
1. 연속된 수들의 합중 가장 큰 값 D[N]
arr[] = {10,-4,3,1,5,6,-35,12,21,-1}; 과
D[0] ={10,
D[1] = max(10-4,arr[1])
D[2] = max(D[1],arr[2])
D[3] = max(D[2],arr[3])
따라서 D[N] = max(D[N-1],arr[N]);
2.나머지 구현
#include<iostream>
#include<algorithm>
using namespace std;
int arr[100001];
int d[100001];
int main(void)
{
int n;
cin >> n;
for (int i = 1; i <= n; ++i)
{
cin >> arr[i];
}
d[1] = arr[1];
for (int i = 2; i <= n; ++i)
{
//d[i] = max(d[i - 1] + arr[i], arr[i]);
if (d[i - 1] + arr[i] < arr[i])
{
d[i] = arr[i];
}
else
{
d[i] = d[i - 1] + arr[i];
}
}
int ans = -1001;
for (int i = 1; i <= n; ++i)
{
if (ans < d[i])
ans = d[i];
}
cout << ans << '\n';
return 0;
}300x250
'Algorithm > 동적계획법(DP)' 카테고리의 다른 글
| 1149 RGB 거리 (복기) (0) | 2020.03.20 |
|---|---|
| 1699 제곱수의 합 (0) | 2020.03.19 |
| 15990 1,2,3 더하기 5 (0) | 2020.03.19 |
| 16194 카드 구매하기 2 (0) | 2020.03.19 |
| 2193 이친수 (0) | 2020.03.17 |




댓글