https://www.acmicpc.net/problem/11054
11054번: 가장 긴 바이토닉 부분 수열
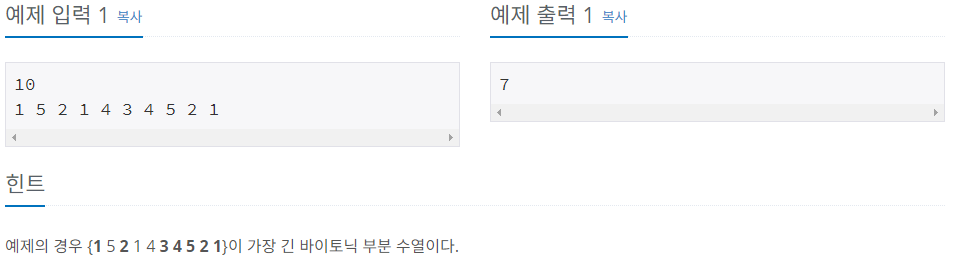
첫째 줄에 수열 A의 크기 N이 주어지고, 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ N ≤ 1,000, 1 ≤ Ai ≤ 1,000)
www.acmicpc.net
가장 긴 바이토닉 부분 수열 성공
시간 제한메모리 제한제출정답맞은 사람정답 비율
| 1 초 | 256 MB | 12899 | 6693 | 5434 | 52.803% |
문제
수열 S가 어떤 수 Sk를 기준으로 S1 < S2 < ... Sk-1 < Sk > Sk+1 > ... SN-1 > SN을 만족한다면, 그 수열을 바이토닉 수열이라고 한다.
예를 들어, {10, 20, 30, 25, 20}과 {10, 20, 30, 40}, {50, 40, 25, 10} 은 바이토닉 수열이지만, {1, 2, 3, 2, 1, 2, 3, 2, 1}과 {10, 20, 30, 40, 20, 30} 은 바이토닉 수열이 아니다.
수열 A가 주어졌을 때, 그 수열의 부분 수열 중 바이토닉 수열이면서 가장 긴 수열의 길이를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 수열 A의 크기 N이 주어지고, 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ N ≤ 1,000, 1 ≤ Ai ≤ 1,000)
출력
첫째 줄에 수열 A의 부분 수열 중에서 가장 긴 바이토닉 수열의 길이를 출력한다.
<풀이>
1. 풀이는 LIS와 가장 긴 감소 수열 풀이를 응용해서 풀 수 있다.
2. 주의할 점은, LIS를 구하고 조건의 부등호만 바꿔서 LDS를 구한다음 둘이 합치려면 합칠 수가 없다.
반례 {3,2,1,4,5,6}
3. 또한 처음에 여럿 실수하는 부분중에, 가장 긴 증가부분을 구하고 거기서부터 감소를 하면 되지 않을까 했지만, {1,5,4,2,3} 같은 경우 가장 끝이 가장 긴 증가 부분 수열이지만 감소를 구하면
길이가 나오지않아 바이토닉을 구할 수 없게된다.
4. 또 다른 반례 {3,4,5,2,1} 이걸 통해 단순 LIS LDS를 합치면 안됨.
5. 풀이로 D1에서 LIS를 구하고, D2 역으로 긴 부분을 구한다음
a1, a2 , a3 , ...... i ...... aN
각 a1부터 an 까지 두 길이의 합과 교차점을 빼주어
최대값이 되는 부분 (가장 긴 바이토닉 수열)을 찾아준다.
#include<iostream>
using namespace std;
int arr[1001];
int d[1001];
int d2[1001];
int main(void)
{
int N;
cin >> N;
for (int i = 1; i <= N; ++i)
{
cin >> arr[i];
}
//LIS
for (int i = 1; i <= N; ++i)
{
d[i] = 1;
for (int k = 1; k <= N; ++k)
{
if (arr[i] > arr[k] && d[i] < d[k] + 1)
{
d[i] = d[k] + 1;
}
}
}
//LDS
for (int i = N; i >= 1; i--)
{
d2[i] = 1;
for (int k = N; k >= 1; k--)
{
if (arr[i] > arr[k] && d2[i] < d2[k] + 1)
{
d2[i] = d2[k] + 1;
}
}
}
int ans = 0;
for (int i = 1; i <= N; ++i)
{
if (ans < d[i] + d2[i] - 1)
ans = d[i] + d2[i] - 1;
}
cout << ans << '\n';
return 0;
}
'Algorithm > 동적계획법(DP)' 카테고리의 다른 글
| 17404 RGB거리 2 (0) | 2020.03.26 |
|---|---|
| 13398 연속합 2 (0) | 2020.03.26 |
| 11722 가장 긴 감소하는 부분 수열 (0) | 2020.03.26 |
| 11055 가장 큰 증가 부분 수열 (0) | 2020.03.26 |
| 1932 정수 삼각형 (0) | 2020.03.24 |




댓글