https://www.acmicpc.net/problem/14888
14888번: 연산자 끼워넣기
첫째 줄에 수의 개수 N(2 ≤ N ≤ 11)가 주어진다. 둘째 줄에는 A1, A2, ..., AN이 주어진다. (1 ≤ Ai ≤ 100) 셋째 줄에는 합이 N-1인 4개의 정수가 주어지는데, 차례대로 덧셈(+)의 개수, 뺄셈(-)의 개수, 곱셈(×)의 개수, 나눗셈(÷)의 개수이다.
www.acmicpc.net
연산자 끼워넣기 성공
시간 제한메모리 제한제출정답맞은 사람정답 비율
| 2 초 | 512 MB | 22378 | 11200 | 7297 | 47.581% |
문제
N개의 수로 이루어진 수열 A1, A2, ..., AN이 주어진다. 또, 수와 수 사이에 끼워넣을 수 있는 N-1개의 연산자가 주어진다. 연산자는 덧셈(+), 뺄셈(-), 곱셈(×), 나눗셈(÷)으로만 이루어져 있다.
우리는 수와 수 사이에 연산자를 하나씩 넣어서, 수식을 하나 만들 수 있다. 이때, 주어진 수의 순서를 바꾸면 안 된다.
예를 들어, 6개의 수로 이루어진 수열이 1, 2, 3, 4, 5, 6이고, 주어진 연산자가 덧셈(+) 2개, 뺄셈(-) 1개, 곱셈(×) 1개, 나눗셈(÷) 1개인 경우에는 총 60가지의 식을 만들 수 있다. 예를 들어, 아래와 같은 식을 만들 수 있다.
- 1+2+3-4×5÷6
- 1÷2+3+4-5×6
- 1+2÷3×4-5+6
- 1÷2×3-4+5+6
식의 계산은 연산자 우선 순위를 무시하고 앞에서부터 진행해야 한다. 또, 나눗셈은 정수 나눗셈으로 몫만 취한다. 음수를 양수로 나눌 때는 C++14의 기준을 따른다. 즉, 양수로 바꾼 뒤 몫을 취하고, 그 몫을 음수로 바꾼 것과 같다. 이에 따라서, 위의 식 4개의 결과를 계산해보면 아래와 같다.
- 1+2+3-4×5÷6 = 1
- 1÷2+3+4-5×6 = 12
- 1+2÷3×4-5+6 = 5
- 1÷2×3-4+5+6 = 7
N개의 수와 N-1개의 연산자가 주어졌을 때, 만들 수 있는 식의 결과가 최대인 것과 최소인 것을 구하는 프로그램을 작성하시오.
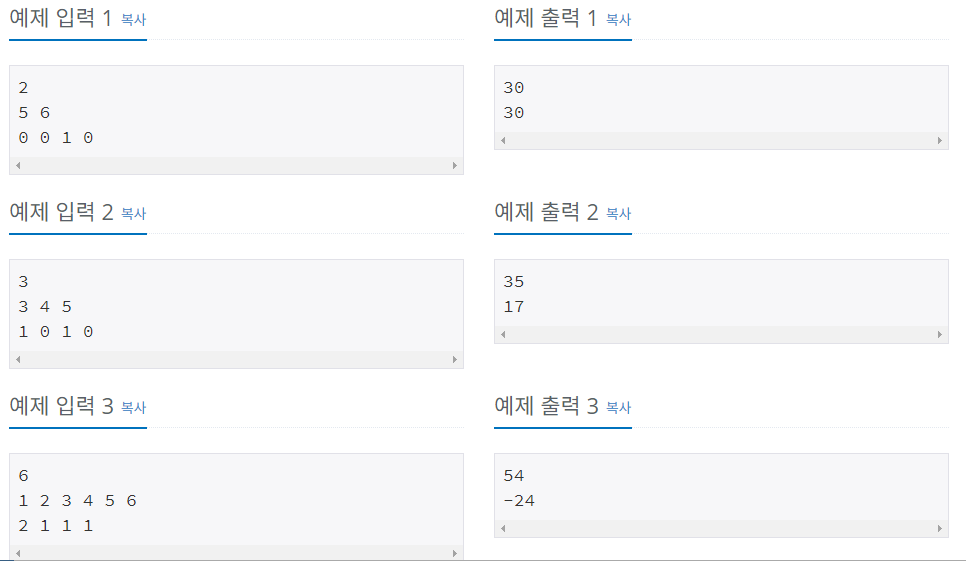
입력
첫째 줄에 수의 개수 N(2 ≤ N ≤ 11)가 주어진다. 둘째 줄에는 A1, A2, ..., AN이 주어진다. (1 ≤ Ai ≤ 100) 셋째 줄에는 합이 N-1인 4개의 정수가 주어지는데, 차례대로 덧셈(+)의 개수, 뺄셈(-)의 개수, 곱셈(×)의 개수, 나눗셈(÷)의 개수이다.
출력
첫째 줄에 만들 수 있는 식의 결과의 최댓값을, 둘째 줄에는 최솟값을 출력한다. 최댓값과 최솟값이 항상 -10억보다 크거나 같고, 10억보다 작거나 같은 결과가 나오는 입력만 주어진다. 또한, 앞에서부터 계산했을 때, 중간에 계산되는 식의 결과도 항상 -10억보다 크거나 같고, 10억보다 작거나 같다.
힌트
세 번째 예제의 경우에 다음과 같은 식이 최댓값/최솟값이 나온다.
- 최댓값: 1-2÷3+4+5×6
- 최솟값: 1+2+3÷4-5×6
<풀이>
1. 연산자의 갯수는 수의 개수-1개이다. 최대 10개가 올 수 있고.
연산자의 10개의 순서를 바꿔가며 경우의 수를 따져볼때 10!에 모든 경우의 수를 찾을 수 있다.
2. 연산자를 +, - , *, / 를 각 구분지어서 리스트에 담았다.
3. 정렬이 필요한 경우 정렬, (가장 작은수부터 인덱스를 집어넣으면 상관없음)
4. 정렬된 연산자들을 구분지어 놓은 집합의 원소들의 다음순열을 찾아가며 수에 모두 대입.
5. 대입된 수에서 최댓값을 찾고, 최솟값을 찾는다.
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int N;
int arr[11];
vector <int>v;
int main(void)
{
cin >> N;
for (int i = 0; i < N; ++i)
{
cin >> arr[i];
}
for (int i = 0; i < 4; ++i)
{
int n;
cin >> n;
for (int k = 0; k < n; ++k)
{
v.push_back(i);
}
}
//0: +
//1: -
//2: x
//3: /
int ans_max = -1e9;
int ans_min = 1e9;
do {
int sum = arr[0];
for (int i = 1,k=0; i < N; ++i)
{
if (v[k] == 0) sum += arr[i];
else if (v[k] == 1) sum -= arr[i];
else if (v[k] == 2) sum *= arr[i];
else if (v[k] == 3) sum /= arr[i];
k += 1;
}
if (ans_max < sum) ans_max = sum;
if (ans_min > sum) ans_min = sum;
} while (next_permutation(v.begin(), v.end()));
cout << ans_max << '\n' << ans_min << '\n';
return 0;
}'Algorithm > 완전탐색(BruteForce)' 카테고리의 다른 글
| 6603 로또(재귀 풀이) (0) | 2020.04.01 |
|---|---|
| 14889 스타트와 링크 (순열 풀이) (0) | 2020.04.01 |
| 1339 단어 수학(순열 풀이) (0) | 2020.04.01 |
| 2529 부등호 (순열 풀이) (0) | 2020.03.27 |
| 1182 부분수열의 합 (0) | 2020.03.13 |




댓글